Eliminación
La estrategia para diseñar el algoritmo de eliminación sobre árboles AVL es la misma que para la inserción: Se utiliza el mismo algoritmo que sobre árboles binarios de búsqueda, pero en cada recursión se detectan y corrijen errores por medio de balancear() y se actualiza la altura del nodo actual.
Recordamos un poco la idea del algoritmo de eliminación sobre árboles binarios de búsqueda. Primero se recorre el árbol para detectar el nodo a eliminar. Una vez hecho esto hay tres casos a diferenciar por su complejidad:
Si dicho nodo es una hoja procedemos a eliminarlos de inmediato, sin más.
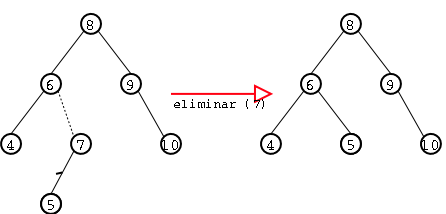
Si dicho nodo tiene un sólo hijo, el nodo puede eliminarse después de ajustar un apuntador del padre para saltar el nodo. Esto se muestra en Figure 13.
Si dicho nodo tiene dos hijos el caso es un poco más complicado. Lo que se estila hacer (y que de hecho se hace en el algoritmo gracias a la función auxiliar eliminar_min()) reemplazar el nodo actual por el menor nodo de su subárbol derecho (y luego eliminar éste).
void eliminar (AVLTree ** t, int x);
/* elimina x del árbol en un tiempo O(log(n)) peor caso.
Precondición: existe un nodo con valor x en el árbol
t. */
int eliminar_min (AVLTree ** t);
/* Función auxiliar a eliminar(). Elimina el menor nodo del árbol
*t devolviendo su contenido (el cual no se libera de
memoria). Se actualizan las alturas de los nodos.
Precondición: !es_vacio(*t) */
void
eliminar (AVLTree ** t, int x)
{
AVLTree *aux;
if (x < raiz (*t))
eliminar (&(*t)->izq, x);
else if (x > raiz (*t))
eliminar (&(*t)->der, x);
else /* coincidencia! */
{
if (es_vacio (izquierdo (*t)) && es_vacio (derecho (*t)))
{/* es una hoja */
free (*t);
(*t) = vacio();
}
else if (es_vacio (izquierdo (*t)))
{/* subárbol izquierdo vacio */
aux = (*t);
(*t) = (*t)->der;
free (aux);
}
else if (es_vacio (derecho (*t)))
{/* subárbol derecho vacio */
aux = (*t);
(*t) = (*t)->izq;
free (aux);
}
else /* caso más complicado */
{
(*t)->dato = eliminar_min (&(*t)->der);
}
}
balancear (t);
actualizar_altura (*t);
}
int
eliminar_min (AVLTree ** t)
{
if (es_vacio (*t))
{
fprintf (stderr,
"No se respeta precondición de eliminar_min()\n");
exit(0);
}
else
{
if (!es_vacio (izquierdo (*t)))
{
int x = eliminar_min (&(*t)->izq);
balancear (t);
actualizar_altura (*t);
return x;
}
else
{
AVLTree *aux = (*t);
int x = raiz (aux);
*t = derecho (*t);
free (aux);
balancear (t);
actualizar_altura (*t);
return x;
}
}
}
|