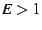 ,
,
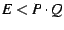 ,
,
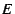 y
y
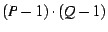 sean co-primos (no tengan factores primos
distintos de
sean co-primos (no tengan factores primos
distintos de 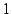 en común o, lo que es equivalente, su máximo común
divisor sea
en común o, lo que es equivalente, su máximo común
divisor sea 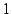 )14.
)14.
Es realmente muy simple, como puede verse a continuación (¡utiliza solamente aritmética modular!):
La clave pública puede difundirse libremente, ya que no se conoce
una forma simple de calcular ![]() ,
, ![]() o
o ![]() dados solamente
dados solamente ![]() y
y ![]() .
.
Para calcular ![]() es necesario calcular
es necesario calcular ![]() y
y ![]() . Dado que sólo
conocemos
. Dado que sólo
conocemos ![]() , y gracias al teorema fundamental de la aritmética16, podemos factorizar este número para descubrir
, y gracias al teorema fundamental de la aritmética16, podemos factorizar este número para descubrir ![]() y
y ![]() . El inconveniente
radica en que la forma más eficiente de factorizar un número
. El inconveniente
radica en que la forma más eficiente de factorizar un número ![]() que se conoce en la actualidad17 es
que se conoce en la actualidad17 es ![]() . Esto significa que toma una cantidad de tiempo exponencial
respecto del tamaño del número a factorizar. Si
. Esto significa que toma una cantidad de tiempo exponencial
respecto del tamaño del número a factorizar. Si ![]() y
y ![]() son dos
enteros cuya representación binaria ocupa
son dos
enteros cuya representación binaria ocupa ![]() bits, factorizar
su producto puede llevarle a cualquier computadora varios milenios,
como mínimo (esto sin tener en cuenta el espacio necesario para realizar
los cálculos).
bits, factorizar
su producto puede llevarle a cualquier computadora varios milenios,
como mínimo (esto sin tener en cuenta el espacio necesario para realizar
los cálculos).