detectseparation provides pre-fit and post-fit methods for the detection of separation and of infinite maximum likelihood estimates in binomial response generalized linear models.
The key methods are detect_separation and
check_infinite_estimates.
You can install the released version of detectseparation from CRAN with:
install.packages("detectseparation")And the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("ikosmidis/detectseparation")Heinze and Schemper (2002) used a logistic regression model to
analyze data from a study on endometrial cancer (see, Agresti 2015,
Section 5.7 or ?endometrial for more details on the data
set). Below, we refit the model in Heinze and Schemper (2002) in order
to demonstrate the functionality that detectseparation
provides.
library("detectseparation")
data("endometrial", package = "detectseparation")
endo_glm <- glm(HG ~ NV + PI + EH, family = binomial(), data = endometrial)
theta_mle <- coef(endo_glm)
summary(endo_glm)
#>
#> Call:
#> glm(formula = HG ~ NV + PI + EH, family = binomial(), data = endometrial)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -1.50137 -0.64108 -0.29432 0.00016 2.72777
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 4.30452 1.63730 2.629 0.008563 **
#> NV 18.18556 1715.75089 0.011 0.991543
#> PI -0.04218 0.04433 -0.952 0.341333
#> EH -2.90261 0.84555 -3.433 0.000597 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 104.903 on 78 degrees of freedom
#> Residual deviance: 55.393 on 75 degrees of freedom
#> AIC: 63.393
#>
#> Number of Fisher Scoring iterations: 17The maximum likelihood (ML) estimate of the parameter for
NV is actually infinite. The reported, apparently finite
value is merely due to false convergence of the iterative estimation
procedure. The same is true for the estimated standard error, and, hence
the value
r round(coef(summary(endo_glm))["NV", "z value"], 3) for
the z-statistic cannot be trusted for inference on the size of
the effect for NV.
detect_separationdetect_separation is pre-fit method, in the
sense that it does not need to estimate the model to detect separation
and/or identify infinite estimates. For example
endo_sep <- glm(HG ~ NV + PI + EH, data = endometrial,
family = binomial("logit"),
method = "detect_separation")
endo_sep
#> Implementation: ROI | Solver: lpsolve
#> Separation: TRUE
#> Existence of maximum likelihood estimates
#> (Intercept) NV PI EH
#> 0 Inf 0 0
#> 0: finite value, Inf: infinity, -Inf: -infinitySo, the actual maximum likelihood estimates are
coef(endo_glm) + coef(endo_sep)
#> (Intercept) NV PI EH
#> 4.3045178 Inf -0.0421834 -2.9026056and the estimated standard errors are
coef(summary(endo_glm))[, "Std. Error"] + abs(coef(endo_sep))
#> (Intercept) NV PI EH
#> 1.63729861 Inf 0.04433196 0.84555156check_infinite_estimatesLesaffre and Albert (1989, Section 4) describe a procedure that can
hint on the occurrence of infinite estimates. In particular, the model
is successively refitted, by increasing the maximum number of allowed
iteratively re-weighted least squares iterations at east step. The
estimated asymptotic standard errors from each step are, then, divided
to the corresponding ones from the first fit. If the sequence of ratios
diverges, then the maximum likelihood estimate of the corresponding
parameter is minus or plus infinity. The following code chunk applies
this process to endo_glm.
(inf_check <- check_infinite_estimates(endo_glm))
#> (Intercept) NV PI EH
#> [1,] 1.000000 1.000000e+00 1.000000 1.000000
#> [2,] 1.424352 2.092407e+00 1.466885 1.672979
#> [3,] 1.590802 8.822303e+00 1.648003 1.863563
#> [4,] 1.592818 6.494231e+01 1.652508 1.864476
#> [5,] 1.592855 7.911035e+02 1.652591 1.864492
#> [6,] 1.592855 1.588973e+04 1.652592 1.864493
#> [7,] 1.592855 5.298760e+05 1.652592 1.864493
#> [8,] 1.592855 2.332822e+07 1.652592 1.864493
#> [9,] 1.592855 2.332822e+07 1.652592 1.864493
#> [10,] 1.592855 2.332822e+07 1.652592 1.864493
#> [11,] 1.592855 2.332822e+07 1.652592 1.864493
#> [12,] 1.592855 2.332822e+07 1.652592 1.864493
#> [13,] 1.592855 2.332822e+07 1.652592 1.864493
#> [14,] 1.592855 2.332822e+07 1.652592 1.864493
#> [15,] 1.592855 2.332822e+07 1.652592 1.864493
#> [16,] 1.592855 2.332822e+07 1.652592 1.864493
#> [17,] 1.592855 2.332822e+07 1.652592 1.864493
#> [18,] 1.592855 2.332822e+07 1.652592 1.864493
#> [19,] 1.592855 2.332822e+07 1.652592 1.864493
#> [20,] 1.592855 2.332822e+07 1.652592 1.864493
#> attr(,"class")
#> [1] "inf_check"
plot(inf_check)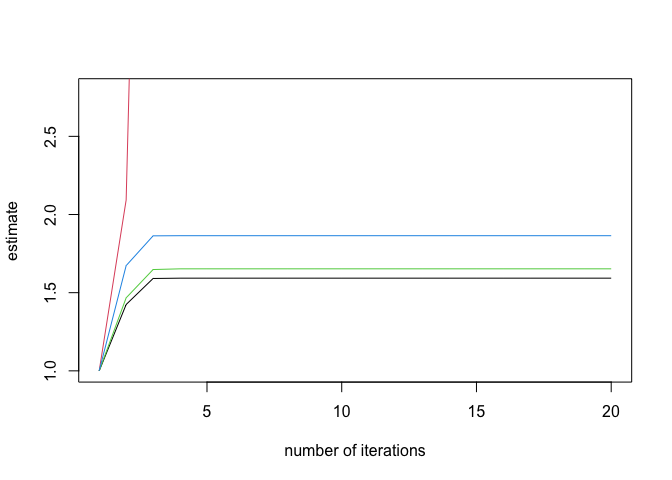
Agresti, A. 2015. Foundations of Linear and Generalized Linear Models. Wiley Series in Probability and Statistics. Wiley.
Heinze, G., and M. Schemper. 2002. “A Solution to the Problem of Separation in Logistic Regression.” Statistics in Medicine 21: 2409–19.
Lesaffre, E., and A. Albert. 1989. “Partial Separation in Logistic Discrimination.” Journal of the Royal Statistical Society. Series B (Methodological) 51 (1): 109–16. https://www.jstor.org/stable/2345845.