LinuxFocus article number 345 http://linuxfocus.org

von Ralf Wieland <rwieland(at)zalf.de> Über den Autor: Ich beschäftige mich mit Umweltsimulation, neuronalen Netzen und Fuzzy-Systemen, indem ich sie programmiere. Letzteres vollzieht sich immer unter Linux (seit 0.99pl12). Weiterhin bin ich an Elektronik und Hardware interessiert und versuche, das mit Linux zu verbinden.

Linux in der Wissenschaft - oder wie ein nützliches Neuronales Netzwerk Tool entstand Zusammenfassung: Der Artikel zeigt die Eignung linux basierter Software in der Wissenschaft. Besonders Bezug genommen wird dabei auf die Entwicklung wissenschaftlicher Tools zur Umweltsimulation. Als Beispiel wird der unter die GPL gestellte neuronale Netzwerksimulator vorgestellt. _________________ _________________ _________________

Worum geht es?

Ich arbeite in einem Forschungsinstitut , das sich mit Landschaftsforschung beschäftigt. Es geht dabei um Fragen wie:

• Können wir das Wasser auch in 50 Jahren noch bedenkenlos trinken?
• Welche Pflanzen und Tiere werden hier leben, wenn sich das Klima ändert, gibt es noch Wald, kann der Acker noch bestellt werden?
• Wohin fliegt der Staub der Wüste und wie breiten sich Wüsten aus?

Die tägliche Kleinarbeit mit Linux

Die tägliche Kleinarbeit, die aus Analyse von Datenreihen, dem Schimpfen über fehlerhafte Messwerte, dem Umformatieren unterschiedlicher Datenformate, dem Schreiben von Berichten etc. besteht, profitiert ganz stark von Linux. Auch wenn einige glauben, man könne mit Excel und Co alles machen, so erweist sich doch die Kombination von Perl, Emacs, octave [www.octave.org], R [www.r-project.org] etc. als starke Waffe im Kampf mit den Daten. Was kann man alles mit PERL anstellen. Nicht nur Datenkonvertierung, auch Datenbankabfrage (MySQL) , Kalkulationen etc. lassen sich damit schnell und reproduzierbar erledigen. Gerade letzteres ist wichtig, da Handarbeit häufig Fehler in die Daten einbringt, was mit ausgetesteten Skripten wesentlich seltener der Fall ist. Auch das Schreiben von Artikeln mit LaTeX überzeugt durch Qualität. Linux liefert Tools, die es als wissenschaftliches Arbeitsmittel empfehlenswert machen. Ein Nachteil soll aber nicht verschwiegen werden: man muss sich mit den Tools intensiv beschäftigen. Nicht alles ist intuitiv und nicht jeder ist ein Programmierfreak.

Die andere Seite - Toolentwicklung

Warum muss man überhaupt selbst entwickeln, es gibt doch alles? In der Simulation gibt es leistungsstarke Tools wie Matlab [www.mathworks.com] . Für die Behandlung geographischer Daten gibt es Geographische Informationssystem (GIS) wie ARCGIS [www.esri.com/software/arcgis] oder als freie Software Grass [grass.itc.it] . Für die Statistik sieht es nicht anders aus. Also warum noch entwickeln?
Hier liegt das Problem nicht in der Leistungsfähigkeit der Einzelkomponenten, sondern im System des Zusammenwirkens. Für eine Simulation müssen Teilaufgaben in unterschiedlichen Programmen abgearbeitet werden, die aber nur umständlich, d.h. über selbstzuschreibende Interfaces miteinander kommunizieren können. Weiterhin kommt erschwerend hinzu, dass die Daten immer als Massendaten (räumliche Daten) mit hoher Fehlerrate vorliegen. Die erforderlichen Simulationen müssen diesem Charakter Rechnung tragen. Ein Algorithmus muss auch dann noch sinnvolle Werte liefern, wenn die Eingangsdaten nicht stimmig sind, bzw. er muss hier warnen. Die Verarbeitung von Massendaten (Matrizen mit mehr als einer Million Elemente sind eher die Regel) erfordern schnelle Algorithmen. Robuste und schnelle Algorithmen lassen sich oft nur in Eigenentwicklung implementieren.
Die wesentlichste Schwäche kommerzieller Systeme ist aber die Geheimhaltung des Quellcodes. Wie sollen Wissenschaftler denn Modelle entwickeln und austauschen, wenn die Quellen nicht offen liegen? Aus dieser Analyse wurde beschlossen, ein eigenes "Spatial Analysis and Modeling Tool" (SAMT) als Open Source Software zu entwickeln.
Es ist ein Simulationstool, das eine eigene Datenhaltung für räumliche Daten, Schnittstellen zur Datenbank MySQL und zum GIS besitzt. Es enthält grundlegende Funktionen zur Verwaltung rasterbasierter Daten, es kann Raster manipulieren (Verschneiden, Distanzen, Interpolation etc.) und es kann diese Daten sowohl zweidimensional als auch dreidimensional präsentieren.
Bemerkung: Rasterdaten basieren auf der Einteilung einer Karte in kleine Planquadrate. Die Informationen sind in mehreren Ebenen solcher Rasterdaten gespeichert. Ein Modell greift auf die Informationen der Ebenen zu. Neben diesen in die Tiefe gehenden Informationen sind aber auch die Umgebung eines Rasters in der gleichen Ebene wichtig. Letzteres bildet die Grundlage für die Modellierung von lateralen Stoffflüssen, wie sie z.B. bei der Bodenerosion durch Wind und Wasser auftreten.
SAMT bildet den Rahmen, in den sich Tools wie ein (sehr schneller) Fuzzyinterpreter und das neuronale Netztool (nnqt) einpassen lassen. Fuzzymodelle dienen der Einbeziehung von Expertenwissen in die Simulation. Häufig kann ein Experte einen Prozess beschreiben oder auch steuern, auch wenn kein mathematisches Modell vorliegt. Mit neuronalen Netzen sind Verfahren gemeint, die es erlauben, aus Messdaten funktionale Zusammenhänge abzuleiten. Im weiteren soll die Entwicklung des neuronalen Netztools vorgestellt werden.

Was ist ein neuronales Netz?

Ein (künstliches) neuronales Netz besteht aus mehreren Ebenen. Die erste Ebene wird mit den zu trainierenden Eingangsdaten in Form von Gleitkommazahlen beschickt. Die Ebene zwischen Input und Output ist nach aussen nicht direkt sichtbar und wird hidden layer genannt. Manchmal gibt es auch mehrere hidden layer. Die abschließende Ebene besteht im Beispiel nur aus einem Element. Eine solche Architektur wird genutzt, um eine Funktion aus mehreren Inputs und einem Output nachzubilden. Die hidden layer sind notwendig, um nichtlineares Verhalten abbilden zu können, beispielsweise die Funktion x^2-y^2. Wie kann aber ein Netz die gewünschte Funktion kennen? Am Anfang kennt das Netz die Funktion natürlich nicht. Die Verbindungen (Wichtungen) zwischen den Elementen (Knoten) werden mit zufälligen Werten belegt. Im Verlauf des Trainigsprozesse versucht der Lernalgorithmus die Gewichte so zu verändern, dass der mittlere quadratische Fehler zwischen dem berechneten und dem vorgegebenen Output minimal wird. Dazu gibt es eine Vielzahl von Algorithmen, auf die hier aber nicht eingegangen werden soll. In nnqt wurden drei Algorithmen implementiert. Bedingt durch die Vorgabe des gewünschten Outputs spricht man bei diesem Trainingsprozess auch vom überwachten Lernen (supervised learning).

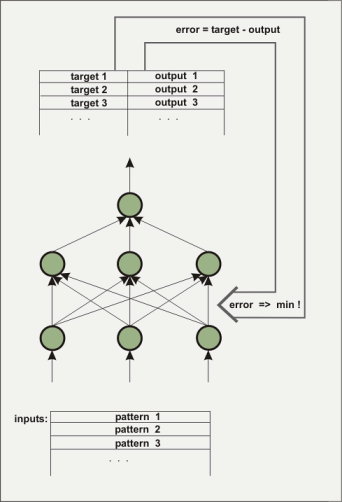
Das Netz ist trainiert, wenn es einen genügend kleinen Fehler sowohl bei den Trainingsdaten als auch bei den Kontrolldaten (Man trennt zweckmäßigerweise einen Teil der Daten vor dem Training ab und nutzt diesen Teil als Kontrolldaten für die Überprüfung des Lernverhaltens.) erreicht hat. Die Wichtungen bestimmen das Verhalten des Netzes und werden für die Verwendung gespeichert. Was kann man alles mit so einem Netz anstellen? Neben dem Einsatz in der Wissenschaft als Modelltool, gibt es auch eine Reihe von Einsatzgebieten, die mehr oder weniger ernst zu nehmen sind. So gibt es Versuche, mit solchen Netzen Kursverläufe an der Börse vorherzusagen. Mir ist so etwas bisher noch nicht gelungen, aber vielleicht gelingt es jemandem.
Eine für mich interessante Möglichkeit ergibt sich, wenn man ein neuronales Netz zur kurzfristigen Wettervorhersage nutzt. So können beispielsweise die Daten elektronischer Wetterstationen genutzt werden, um damit ein neuronales Netz zu trainieren. Interessant sind dabei vor allem der Luftdruck und die Veränderung des Luftdrucks bzgl. der Regenereignisse. Die Symbole auf den Wetterstationen werden nach solchen Mustern angezeigt. Vielleicht kann es ein neuronales Netz besser? Um eigene Experimente zu unterstützen, steht nnqt als gpl-Software zur Verfügung.

Das neuronale Netztool nnqt

Den Anstoß zur Entwicklung des neuronalen Netztools gaben Wissenschaftler, die mit dem Wunsch an mich herantraten, ihre erhobenen Daten zu untersuchen. Sie wollten ein möglichst einfaches Tool, das sie aber auch im räumlichen Kontext nutzen können. D.h. sie wollten sehen, wie die Ergebnisse im Raum liegen. Natürlich gibt es sehr gute neuronale Netztools auf dem Markt. Auch freie Tools, wie SNNS [www-ra.informatik.uni-tuebingen.de/SNNS/] , oder auch Softwarebibliotheken wie, fann [fann.sourceforge.net] liegen vor. SNNS ist phantastisch, aber es kann eben nicht so einfach von jemanden genutzt werden, der nicht programmiert, da es C-Quelltext als output liefert. Auch ist es in seinem Umfang für einen Gelegenheitsnutzer wohl zu überwältigend. Für nnqt gab es eine Reihe von Forderungen, die erfüllt werden sollten:

• Integration in SAMT (Nutzung von Rasterdaten als Trainingsets), Verwendung der gespeicherten Netze als räumliche Modelle
• Interaktive Bedienung, Integration von Analysetechniken
• Nutzung auch als Tool ausserhalb von SAMT

Entwicklung von nnqt

Die Entwicklung vollzog sich dabei in folgenden Schritten:

1. Entwicklung und Test der Algorithmen
2. Implementation als qt-Applikation
3. Integration in SAMT

Entwicklung und Test der Algorithmen

Nun gibt es eine überwältigende Zahl guter Literatur über neuronale Netze. Hier sei stellvertretend nur mal ein Buch genannt. Trotzdem bleibt da manchmal eine Lücke, die man durch eigene Experimente und dem Erfahrungsaustausch mit anderen schließen kann. Mir gefiel die schnelle Arbeit mit Matlab unter Verwendung des Levenberg-Marquardt-Algorithmus. Erst durch intensive Suche im Internet entdeckte ich einen Artikel [www.eng.auburn.edu/~wilambm/pap/2001/FastConv_IJCNN01.PDF][local copy, 105533 bytes] der diesen Algorithmus auf neuronale Netze angewandt hat. Das war die Basis. Ich hatte "nur" noch die Aufgaben die von mir favorisierte tanh (Tangens Hyperbolicus) Funktion in den Algorithmus einzupassen. Auch hier nutzte ich wieder Software unter Linux, nämlich das Computeralgebra System Maxima [maxima.sourceforge.net] . Mit einem solchem System kann man komplizierte Gleichungen umformen, kann differenzieren und solche Dinge, die nicht so einfach mit Bleistift und Papier durchzuführen sind. Maxima erlaubte es mir, in einer Wochenendschicht die notwendigen Umformungen durchzuführen und eine erste Version des Algorithmus in C zu implementieren. Diese C-Implementierung diente zum Test und der Parameteroptimierung. Unter Nutzung des Open-Source Simulationssystems desire [members.aol.com/gatmkorn] , vielen herzlichen Dank an den Entwickler Prof. Korn, als Vergleichswerkzeug, konnten erste Modellrechnungen durchgeführt werden. Dabei schlug sich der neu implementierte Algorithmus nicht schlecht. Die Trainingszeiten für das xor-Problem, ein beliebtes Testbeispiel für neuronale Netze, lagen bei durchschnittlich 70ms auf einem Pentium 3GHz Rechner. (Die Zeit wird im wesentlichen durch die Leseoperation von der Festplatte benötigt, so dass auch auf einem älteren Athlon 750 MHz Rechner die Rechenzeit nur knapp darüber lag.)
Alternativ wurde auch der bekannte Backpropagation Algorithmus implementiert und untersucht. Nach diesen Vorarbeiten, die eine Basis für die weitere Verbesserung der Algorithmen bilden (Adaption der Lernparamter als Beispiel) ging es an die Implementierung der Toolbox.

Implementierung und Ergebnisse

Ich bevorzuge qt als Entwicklungsumgebung. QT ist sehr gut dokumentiert, objektorientiert und ich kann emacs als Editor verwenden. Der Designer von qt hilft beim Entwurf der Oberfläche. Trotzdem reichen die Möglichkeiten nicht für die Entwicklung des nnqt. Ich benötige so etwas wie Diagramme, Skalen etc. Auch hier half mir die Entwicklergemeinschaft. So konnten die Bibliotheken qwt [qwt.sourceforge.net] und qwt3d [qwtplot3d.sourceforge.net] genutzt werden, die die Entwicklungszeit drastisch verkürzten. Gewappnet mit diesen Mitteln wurde nnqt in ca. 2 Wochen zusammengebaut. Als ich schon recht zufrieden war, ging ich auf die Anwender zu. Die hatten vielleicht Wünsche! Man wollte die Datenmenge in eine Trainingsmenge und eine Testmenge automatisch splitten, man möchte zur besseren Übersichtlichkeit Namen vergeben können, man möchte weitere Untersuchungen wie Diagramme mit Parameterkurven usw. Na gut, einiges konnte ich sofort integrieren, anderes wird wohl noch etwas dauern. Hier mal ein paar Screenshots:

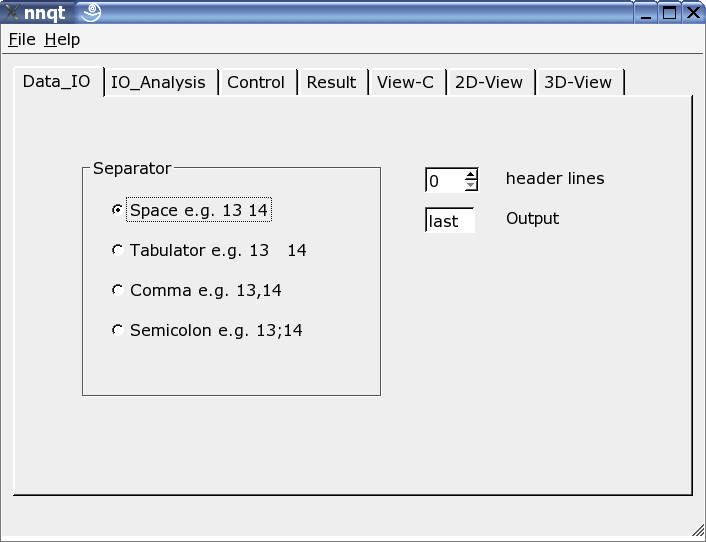
Hier kann der Reader auf das Inputformat der Daten angepasst werden. Es können unterschiedliche Trennzeichen verwendet werden, ein paar Headerzeilen ausgeblendet oder auch die Stelle des Target im Datensatz frei gewählt werden. Bemerkung: man sollte sein Datenformat schon kennen, da nnqt sich hier auf die Nutzerangaben verlässt.

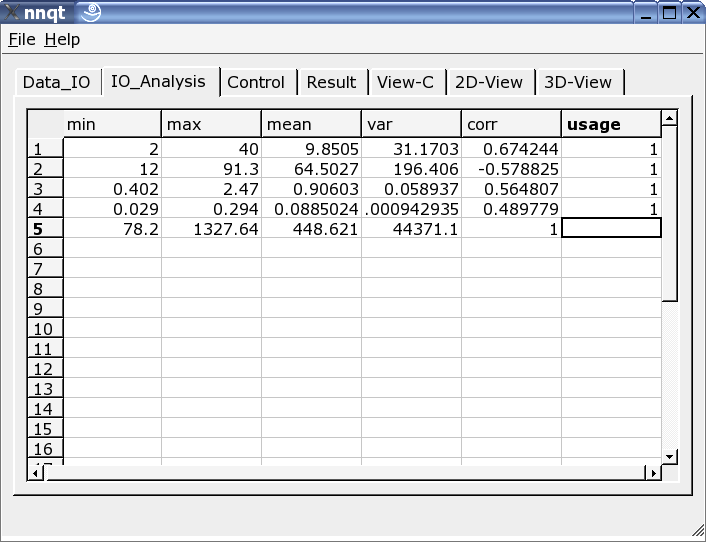
Verlief der Dateninput erfoglreich, so erfolgt sofort der Sprung auf die Datenanalyseseite. Hier gibt es ein paar Informationen zu den Daten und hier werden aus allen Spalten, die für das Training zu verwendenden ausgewählt. Eine 1 in der letzten Spalte markiert den Input als Trainingsgröße. (Es sind bis zu 29 Trainingsgrößen nutzbar.)

Die wichtigste Seite bildet die Control-Seite. Hier werden die Anzahl der Hiddenelemente bestimmt, die Zahl der Lernschritte festgelegt und der Trainingsalgorithmus ausgewählt. Das Training kann an der Thermometerskala oder alternativ als Zahl beobachtet werden. Es ist mehrmals zu trainieren, da die Startparamter zufällig gewählt werden und das Ergebnis sensitiv von diesen abhängt. Der Auswahlknopf "shuffle" bewirkt eine zufällige Auswahl der Trainingsdaten, anstatt einer sequentiellen. Das ist manchmal günstiger. Ist es gelungen, den mittleren quadratischen Fehler genügend zu drücken, kann mittels des "view_trained" Buttons auf die erste graphische Darstellung gesprungen werden:

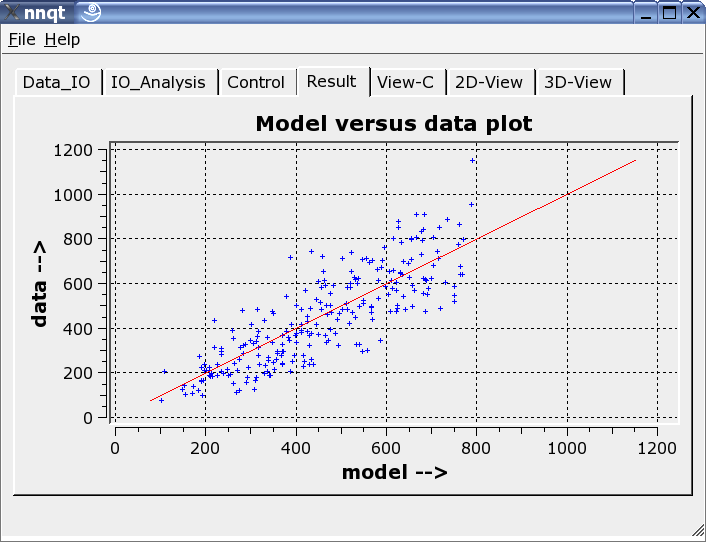
Hier werden die Trainingsdaten mit dem durch das neuronale Netz berechneten Daten verglichen. Idealerweise liegen die Daten auf der Diagonalen. Aber das Ideal ist nicht erreichbar! Trotzdem sehen die Ergebnisse recht ordentlich aus. (Es werden in roter Darstellung übrigens die Kontrolldaten, also die Daten, die nicht trainiert wurden, angezeigt.) Im nächsten Schritt können Funktionsverläufe analysiert werden. Dazu sind die Defaultwerte so einzustellen, dass sie sinnvoll sind. Hier ist entsprechende Sorgfalt walten zu lassen, da die Netze nur in der Nähe ihrer Trainingsdaten zuverlässig arbeiten.

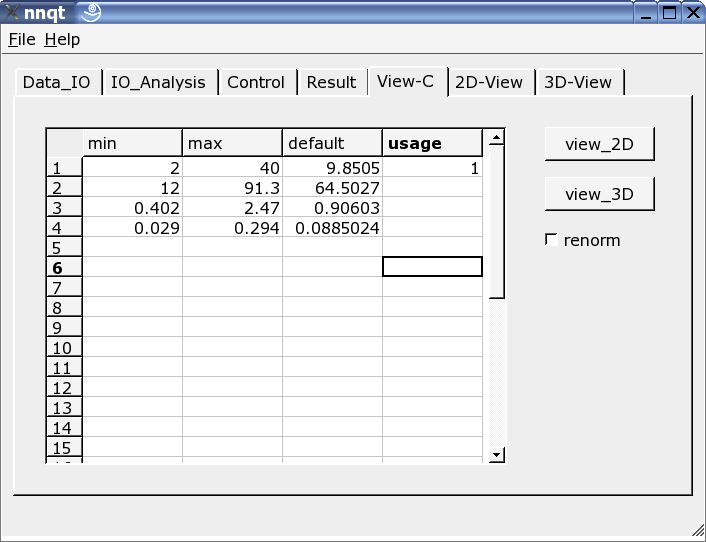
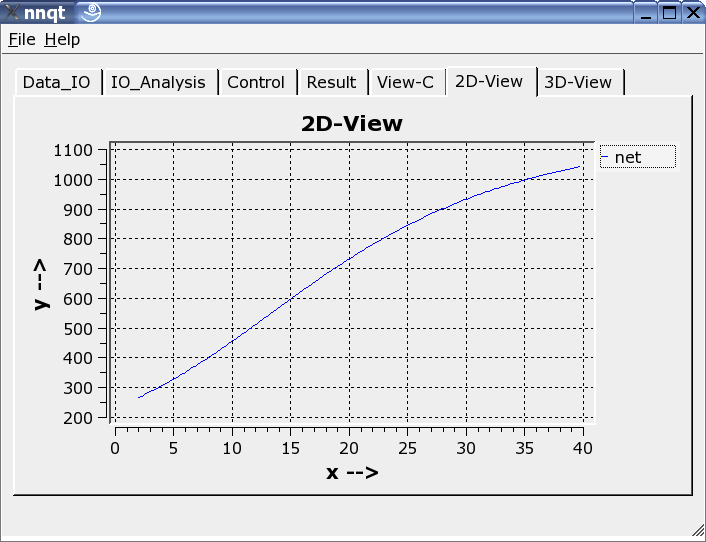
Es können sowohl zweidimensionale Darstellungen als auch dreidimensionale gewählt werden.

Nachnutzung von nnqt

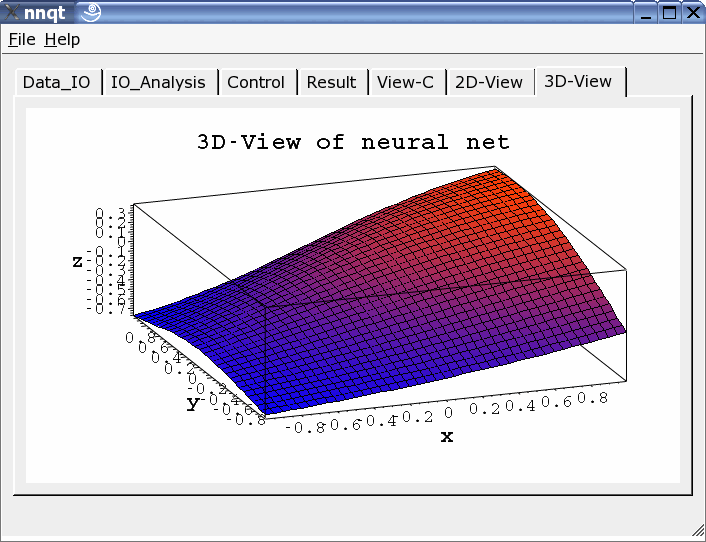
nnqt ist Open Source Software und wurde unter der GPL veröffentlicht. Jeder kann es frei nutzen und verbessern. Letzteres wäre besonders schön. Die Installation ist recht einfach. Es müssen nur die qwt-Libraries installiert werden und natürlich qt muss vorhanden sein bzw. installiert werden. Das nnqt.tgz ist einfach auszupacken (tar -zxvf nnqt.tgz). Dabei entsteht ein neues Verzeichnis nnqt. Mit einem cd nnqt kann im Verzeichnis nnqt ein qmake und ein anschließendes make gestartet werden. Wurde alles fehlerfrei übersetzt,so ist nur noch eine shell-Variable mit:
export NN_HOME=/pfad_zu_nnqt
zu setzen. Wenn jetzt in einem neuen Terminal nnqt gestartet wird, sollten die Daten und Modelle durch nnqt gefunden werden. Damit wünsche ich viel Spaß. Zum Testen gibt es eine Datenreihe mit zwei Inputs mit. Erkennt jemand die Funktion, die gelernt wurde? (Es ist x^2-y^2 im Bereich von [-2..2])

Was kann man nun alles damit machen - ich bin gespannt auf Eure Ideen.

Dank an die Comunity

Es hat sich gezeigt, dass Linux eine ausgezeichnete Entwicklungsumgebung für die Behandlung wissenschaftlicher Probleme ist. Ich konnte auf hervorragender Software aufbauen, ohne die man nie in so kurzer Zeit von ca. 6 Wochen ein brauchbares Tool entwicklen könnte. Es macht auch immer wieder Spaß, wenn man solche Software frei nutzen kann. Deshalb an dieser Stelle ein herzliches Dankeschön an die vielen Entwickler, die mit ihrer Arbeit all die schönen Dinge ermöglichten, die wir unter Linux nutzen können.

Literatur

James A. Freeman:
"Simulating Neural Networks with Mathematica", Addison-Wesley 1994

Download

2005-01-14, generated by lfparser_pdf version 2.51